Search results for: Maxwells equations
754 Adomian Method for Second-order Fuzzy Differential Equation
Authors: Lei Wang, Sizong Guo
Abstract:
In this paper, we study the numerical method for solving second-order fuzzy differential equations using Adomian method under strongly generalized differentiability. And, we present an example with initial condition having four different solutions to illustrate the efficiency of the proposed method under strongly generalized differentiability.
Keywords: Fuzzy-valued function, fuzzy initial value problem, strongly generalized differentiability, adomian decomposition method.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 2537753 The Particle Swarm Optimization Against the Runge’s Phenomenon: Application to the Generalized Integral Quadrature Method
Authors: A. Zerarka, A. Soukeur, N. Khelil
Abstract:
In the present work, we introduce the particle swarm optimization called (PSO in short) to avoid the Runge-s phenomenon occurring in many numerical problems. This new approach is tested with some numerical examples including the generalized integral quadrature method in order to solve the Volterra-s integral equations
Keywords: Integral equation, particle swarm optimization, Runge's phenomenon.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1418752 Modal Approach for Decoupling Damage Cost Dependencies in Building Stories
Authors: Haj Najafi Leila, Tehranizadeh Mohsen
Abstract:
Dependencies between diverse factors involved in probabilistic seismic loss evaluation are recognized to be an imperative issue in acquiring accurate loss estimates. Dependencies among component damage costs could be taken into account considering two partial distinct states of independent or perfectly-dependent for component damage states; however, in our best knowledge, there is no available procedure to take account of loss dependencies in story level. This paper attempts to present a method called "modal cost superposition method" for decoupling story damage costs subjected to earthquake ground motions dealt with closed form differential equations between damage cost and engineering demand parameters which should be solved in complex system considering all stories' cost equations by the means of the introduced "substituted matrixes of mass and stiffness". Costs are treated as probabilistic variables with definite statistic factors of median and standard deviation amounts and a presumed probability distribution. To supplement the proposed procedure and also to display straightforwardness of its application, one benchmark study has been conducted. Acceptable compatibility has been proven for the estimated damage costs evaluated by the new proposed modal and also frequently used stochastic approaches for entire building; however, in story level, insufficiency of employing modification factor for incorporating occurrence probability dependencies between stories has been revealed due to discrepant amounts of dependency between damage costs of different stories. Also, more dependency contribution in occurrence probability of loss could be concluded regarding more compatibility of loss results in higher stories than the lower ones, whereas reduction in incorporation portion of cost modes provides acceptable level of accuracy and gets away from time consuming calculations including some limited number of cost modes in high mode situation.
Keywords: Dependency, story-cost, cost modes, engineering demand parameter.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1019751 A Problem in Microstretch Thermoelastic Diffusive Medium
Authors: Devinder Singh, Arbind Kumar, Rajneesh Kumar
Abstract:
The general solution of the equations for a homogeneous isotropic microstretch thermo elastic medium with mass diffusion for two dimensional problems is obtained due to normal and tangential forces. The Integral transform technique is used to obtain the components of displacements, microrotation, stress and mass concentration, temperature change and mass concentration. A particular case of interest is deduced from the present investigation.
Keywords: Normal and tangential force, Microstretch, thermoelastic, The Integral transform technique.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 2299750 Haar Wavelet Method for Solving Fitz Hugh-Nagumo Equation
Authors: G.Hariharan, K.Kannan
Abstract:
In this paper, we develop an accurate and efficient Haar wavelet method for well-known FitzHugh-Nagumo equation. The proposed scheme can be used to a wide class of nonlinear reaction-diffusion equations. The power of this manageable method is confirmed. Moreover the use of Haar wavelets is found to be accurate, simple, fast, flexible, convenient, small computation costs and computationally attractive.
Keywords: FitzHugh-Nagumo equation, Haar wavelet method, adomain decomposition method, computationally attractive.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 2784749 Lagrangian Method for Solving Unsteady Gas Equation
Authors: Amir Taghavi, kourosh Parand, Hosein Fani
Abstract:
In this paper we propose, a Lagrangian method to solve unsteady gas equation which is a nonlinear ordinary differential equation on semi-infnite interval. This approach is based on Modified generalized Laguerre functions. This method reduces the solution of this problem to the solution of a system of algebraic equations. We also compare this work with some other numerical results. The findings show that the present solution is highly accurate.
Keywords: Unsteady gas equation, Generalized Laguerre functions, Lagrangian method, Nonlinear ODE.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1536748 Extending Global Full Orthogonalization method for Solving the Matrix Equation AXB=F
Authors: Fatemeh Panjeh Ali Beik
Abstract:
In the present work, we propose a new method for solving the matrix equation AXB=F . The new method can be considered as a generalized form of the well-known global full orthogonalization method (Gl-FOM) for solving multiple linear systems. Hence, the method will be called extended Gl-FOM (EGl- FOM). For implementing EGl-FOM, generalized forms of block Krylov subspace and global Arnoldi process are presented. Finally, some numerical experiments are given to illustrate the efficiency of our new method.Keywords: Matrix equations, Iterative methods, Block Krylovsubspace methods.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1997747 Solving of the Fourth Order Differential Equations with the Neumann Problem
Authors: Marziyeh Halimi, Roushanak Lotfikar, Simin Mansouri Borojeni
Abstract:
In this paper we considered the Neumann problem for the fourth order differential equation. First we define the weighted Sobolev space 2 Wα and generalized solution for this equation. Then we consider the existence and uniqueness of the generalized solution, as well as give the description of the spectrum and of the domain of definition of the corresponding operator.Keywords: Neumann problem, weighted Sobolev spaces, generalized solution, spectrum of linear operators.2000 mathematic subject classification: 34A05, 34A30.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1428746 On the Solution of Fully Fuzzy Linear Systems
Authors: Hsuan-Ku Liu
Abstract:
A linear system is called a fully fuzzy linear system (FFLS) if quantities in this system are all fuzzy numbers. For the FFLS, we investigate its solution and develop a new approximate method for solving the FFLS. Observing the numerical results, we find that our method is accurate than the iterative Jacobi and Gauss- Seidel methods on approximating the solution of FFLS.
Keywords: Fully fuzzy linear equations, iterative method, homotopy perturbation method, approximate solutions.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1753745 Modeling of Temperature Fields of Gas Turbine Blades by Considering Heat Flow and Specified Temperature
Authors: C. Ardil
Abstract:
A new mathematical model for calculating the temperature field of the profile part of the cooled blades of gas turbines is developed. The theoretical substantiation of the method is based on the application of the method of potential theory (the method of boundary integral equations). The effectiveness of the implementation of the developed mathematical model is confirmed on the basis of a computational experiment.Keywords: Modeling of temperature fields, gas turbine blades, integral methods, cooled blades, gas turbines.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 662744 Positive Solutions for Boundary Value Problems of Fourth-Order Nonlinear Singular Differential Equations in Banach Space
Authors: Li Xiguang
Abstract:
In this paper, by constructing a special non-empty closed convex set and utilizing M¨onch fixed point theory, we investigate the existence of solution for a class of fourth-order singular differential equation in Banach space, which improved and generalized the result of related paper.
Keywords: Banach space, cone, fixed point index, singular differential equation.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1679743 Stability Analysis of Fractional Order Systems with Time Delay
Authors: Hong Li, Shou-Ming Zhong, Hou-Biao Li
Abstract:
In this paper, we mainly study the stability of linear and interval linear fractional systems with time delay. By applying the characteristic equations, a necessary and sufficient stability condition is obtained firstly, and then some sufficient conditions are deserved. In addition, according to the equivalent relationship of fractional order systems with order 0 < α ≤ 1 and with order 1 ≤ β < 2, one may get more relevant theorems. Finally, two examples are provided to demonstrate the effectiveness of our results.
Keywords: Fractional order systems, Time delay, Characteristic equation.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 3670742 Numerical Solution of Infinite Boundary Integral Equation by Using Galerkin Method with Laguerre Polynomials
Authors: N. M. A. Nik Long, Z. K. Eshkuvatov, M. Yaghobifar, M. Hasan
Abstract:
In this paper the exact solution of infinite boundary integral equation (IBIE) of the second kind with degenerate kernel is presented. Moreover Galerkin method with Laguerre polynomial is applied to get the approximate solution of IBIE. Numerical examples are given to show the validity of the method presented.
Keywords: Approximation, Galerkin method, Integral equations, Laguerre polynomial.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 2184741 The Influence of Gravity on The Temporal Instability of Viscoelastic Liquid Curved Jets
Authors: Abdullah Madhi Alsharif, Jamal Uddin
Abstract:
A liquid curved jet has many applications in different industrial and engineering processes, such as the prilling process for generating small spherical pellets (fertilizer or magnesium). The liquids used are usually molten and contain small quantities of polymers and therefore can be modelled as non-Newtonian liquids. In this paper, we model the viscoelastic liquid jet by using the Oldroyd- B model. An asymptotic analysis has been used to simplify the governing equations. Furthermore, the trajectory and a linear temporal stability in the presence of gravity and rotation have been determined.
Keywords: gravity, prilling, rotation, viscoelastic jets.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1960740 MHD Stagnation Point Flow towards a Shrinking Sheet with Suction in an Upper-Convected Maxwell (UCM) Fluid
Authors: K. Jafar, R. Nazar, A. Ishak, I. Pop
Abstract:
The present analysis considers the steady stagnation point flow and heat transfer towards a permeable shrinking sheet in an upper-convected Maxwell (UCM) electrically conducting fluid, with a constant magnetic field applied in the transverse direction to flow and a local heat generation within the boundary layer, with a heat generation rate proportional to (T-T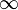 )p Using a similarity transformation, the governing system of partial differential equations is first transformed into a system of ordinary differential equations, which is then solved numerically using a finite-difference scheme known as the Keller-box method. Numerical results are obtained for the flow and thermal fields for various values of the stretching/shrinking parameter λ, the magnetic parameter M, the elastic parameter K, the Prandtl number Pr, the suction parameter s, the heat generation parameter Q, and the exponent p. The results indicate the existence of dual solutions for the shrinking sheet up to a critical value λc whose value depends on the value of M, K, and s. In the presence of internal heat absorption (Q<0) the surface heat transfer rate decreases with increasing p but increases with parameters Q and s when the sheet is either stretched or shrunk.
)p Using a similarity transformation, the governing system of partial differential equations is first transformed into a system of ordinary differential equations, which is then solved numerically using a finite-difference scheme known as the Keller-box method. Numerical results are obtained for the flow and thermal fields for various values of the stretching/shrinking parameter λ, the magnetic parameter M, the elastic parameter K, the Prandtl number Pr, the suction parameter s, the heat generation parameter Q, and the exponent p. The results indicate the existence of dual solutions for the shrinking sheet up to a critical value λc whose value depends on the value of M, K, and s. In the presence of internal heat absorption (Q<0) the surface heat transfer rate decreases with increasing p but increases with parameters Q and s when the sheet is either stretched or shrunk.
Keywords: Magnetohydrodynamic (MHD), boundary layer flow, UCM fluid, stagnation point, shrinking sheet.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 2071739 The Invariant Properties of Two-Port Circuits
Authors: Alexandr A. Penin
Abstract:
Application of projective geometry to the theory of two-ports and cascade circuits with a load change is considered. The equations linking the input and output of a two-port are interpreted as projective transformations which have the invariant as a cross-ratio of four points. This invariant has place for all regime parameters in all parts of a cascade circuit. This approach allows justifying the definition of a regime and its change, to calculate a circuit without explicitly finding the aparameters, to transmit accurately an analogue signal through the unstable two-port.
Keywords: Circuit regime, geometric circuit theory, projective geometry, two-port.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1570738 Adaptive MPC Using a Recursive Learning Technique
Authors: Ahmed Abbas Helmy, M. R. M. Rizk, Mohamed El-Sayed
Abstract:
A model predictive controller based on recursive learning is proposed. In this SISO adaptive controller, a model is automatically updated using simple recursive equations. The identified models are then stored in the memory to be re-used in the future. The decision for model update is taken based on a new control performance index. The new controller allows the use of simple linear model predictive controllers in the control of nonlinear time varying processes.
Keywords: Adaptive control, model predictive control, dynamic matrix control, online model identification
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1779737 Calculation of Voided Slabs Rigidities
Authors: Gee-Cheol Kim, Joo-Won Kang
Abstract:
A theoretical study of the rigidities of slabs with circular voids oriented in the longitudinal and in the transverse direction is discussed. Equations are presented for predicting the bending and torsional rigidities of the voided slabs. This paper summarizes the results of an extensive literature search and initial review of the current methods of analyzing voided slab. The various methods of calculating the equivalent plate parameters, which are necessary for two-dimensional analysis, are also reviewed. Static deflections on voided slabs are shown to be in good agreement with proposed equation.Keywords: voided slab, bending rigidity, torsional rigidity, orthotropic plate
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 3866736 Modification of Rk Equation of State for Liquid and Vapor of Ammonia by Genetic Algorithm
Authors: S. Mousavian, F. Mousavian, V. Nikkhah Rashidabad
Abstract:
Cubic equations of state like Redlich–Kwong (RK) EOS have been proved to be very reliable tools in the prediction of phase behavior. Despite their good performance in compositional calculations, they usually suffer from weaknesses in the predictions of saturated liquid density. In this research, RK equation was modified. The result of this study show that modified equation has good agreement with experimental data.
Keywords: Equation of state, modification, ammonia, genetic algorithm.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 2780735 Existence and Exponential Stability of Almost Periodic Solution for Cohen-Grossberg SICNNs with Impulses
Abstract:
In this paper, based on the estimation of the Cauchy matrix of linear impulsive differential equations, by using Banach fixed point theorem and Gronwall-Bellman-s inequality, some sufficient conditions are obtained for the existence and exponential stability of almost periodic solution for Cohen-Grossberg shunting inhibitory cellular neural networks (SICNNs) with continuously distributed delays and impulses. An example is given to illustrate the main results.
Keywords: Almost periodic solution, exponential stability, neural networks, impulses.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 14334734 Electromagnetic Tuned Mass Damper Approach for Regenerative Suspension
Authors: S. Kopylov, C. Z. Bo
Abstract:
This study is aimed at exploring the possibility of energy recovery through the suppression of vibrations. The article describes design of electromagnetic dynamic damper. The magnetic part of the device performs the function of a tuned mass damper, thereby providing both energy regeneration and damping properties to the protected mass. According to the theory of tuned mass damper, equations of mathematical models were obtained. Then, under given properties of current system, amplitude frequency response was investigated. Therefore, main ideas and methods for further research were defined.
Keywords: Electromagnetic damper, oscillations with two degrees of freedom, regeneration systems, tuned mass damper.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1100733 Calculating Strain Energy in Multi-Surface Models of Cyclic Plasticity
Authors: S. Shahrooi, I. H. Metselaar, Z. Huda
Abstract:
When considering the development of constitutive equations describing the behavior of materials under cyclic plastic strains, different kinds of formulations can be adopted. The primary intention of this study is to develop computer programming of plasticity models to accurately predict the life of engineering components. For this purpose, the energy or cyclic strain is computed in multi-surface plasticity models in non-proportional loading and to present their procedures and codes results.Keywords: Strain energy, cyclic plasticity model, multi-surface model, codes result.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 2093732 A Schur Method for Solving Projected Continuous-Time Sylvester Equations
Authors: Yiqin Lin, Liang Bao, Qinghua Wu, Liping Zhou
Abstract:
In this paper, we propose a direct method based on the real Schur factorization for solving the projected Sylvester equation with relatively small size. The algebraic formula of the solution of the projected continuous-time Sylvester equation is presented. The computational cost of the direct method is estimated. Numerical experiments show that this direct method has high accuracy.Keywords: Projected Sylvester equation, Schur factorization, Spectral projection, Direct method.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1828731 Mathematical Modelling for Separation of Binary Aqueous Solution using Hollow Fiber Reverse Osmosis Module
Authors: Anil Kumar, S. Deswal
Abstract:
The mathematical equation for Separation of the binary aqueous solution is developed by using the Spiegler- Kedem theory. The characteristics of a B-9 hollow fibre module of Du Pont are determined by using these equations and their results are compared with the experimental results of Ohya et al. The agreement between these results is found to be excellent.Keywords: Binary aqueous solution, modeling, reverse osmosis module, Spiegler-Kedem theory.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1643730 Mathematical Modeling of the Influence of Hydrothermal Processes in the Water Reservoir
Authors: Alibek Issakhov
Abstract:
In this paper presents the mathematical model of hydrothermal processes in thermal power plant with different wind direction scenarios in the water reservoir, which is solved by the Navier - Stokes and temperature equations for an incompressible fluid in a stratified medium. Numerical algorithm based on the method of splitting by physical parameters. Three dimensional Poisson equation is solved with Fourier method by combination of tridiagonal matrix method (Thomas algorithm).Keywords: thermal power plant, hydrothermal process, large eddy simulation, water reservoir
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1645729 Conjugate Heat Transfer in an Enclosure Containing a Polygon Object
Authors: Habibis Saleh, Ishak Hashim
Abstract:
Conjugate natural convection in a differentially heated square enclosure containing a polygon shaped object is studied numerically in this article. The effect of various polygon types on the fluid flow and thermal performance of the enclosure is addressed for different thermal conductivities. The governing equations are modeled and solved numerically using the built-in finite element method of COMSOL software. It is found that the heat transfer rate remains stable by varying the polygon types.Keywords: Natural convection, Polygon object, COMSOL
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1890728 Contaminant Transport Modeling Due to Thermal Diffusion Effects with the Effect of Biodegradation
Authors: Nirmala P. Ratchagar, S. Senthamilselvi
Abstract:
The heat and mass transfer characteristics of contaminants in groundwater subjected to a biodegradation reaction is analyzed by taking into account the thermal diffusion (Soret) effects. This phenomenon is modulated mathematically by a system of partial differential equations which govern the motion of fluid (groundwater) and solid (contaminants) particles. The numerical results are presented graphically for different values of the parameters entering into the problem on the velocity profiles of fluid, contaminants, temperature and concentration profile.Keywords: Heat and mass transfer, Soret number, porous media.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1623727 A New Algorithm for Determining the Leading Coefficient of in the Parabolic Equation
Authors: Shiping Zhou, Minggen Cui
Abstract:
This paper investigates the inverse problem of determining the unknown time-dependent leading coefficient in the parabolic equation using the usual conditions of the direct problem and an additional condition. An algorithm is developed for solving numerically the inverse problem using the technique of space decomposition in a reproducing kernel space. The leading coefficients can be solved by a lower triangular linear system. Numerical experiments are presented to show the efficiency of the proposed methods.Keywords: parabolic equations, coefficient inverse problem, reproducing kernel.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 1584726 Explicit Feedback Linearization of Magnetic Levitation System
Authors: Bhawna Tandon, Shiv Narayan, Jagdish Kumar
Abstract:
This study proposes the transformation of nonlinear Magnetic Levitation System into linear one, via state and feedback transformations using explicit algorithm. This algorithm allows computing explicitly the linearizing state coordinates and feedback for any nonlinear control system, which is feedback linearizable, without solving the Partial Differential Equations. The algorithm is performed using a maximum of N-1 steps where N being the dimension of the system.
Keywords: Explicit Algorithm, Feedback Linearization, Nonlinear control, Magnetic Levitation System.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 2976725 Exploring Solutions in Extended Horava-Lifshitz Gravity
Authors: Aziza Altaibayeva, Ertan Gudekli, Ratbay Myrzakulov
Abstract:
In this letter, we explore exact solutions for the Horava-Lifshitz gravity. We use of an extension of this theory with first order dynamical lapse function. The equations of motion have been derived in a fully consistent scenario. We assume that there are some spherically symmetric families of exact solutions of this extended theory of gravity. We obtain exact solutions and investigate the singularity structures of these solutions. Specially, an exact solution with the regular horizon is found.
Keywords: Quantum gravity, Horava-Lifshitz gravity, black hole, spherically symmetric space times.
Procedia APA BibTeX Chicago EndNote Harvard JSON MLA RIS XML ISO 690 PDF Downloads 2249